Dear Students, 
Today we reviewed Ch.18 homework, and Ch.19 Complex Numbers & Ch.20 Absolute Value. Students also worked on the whiteboard about complex number divisions. Here is the class note for your review.
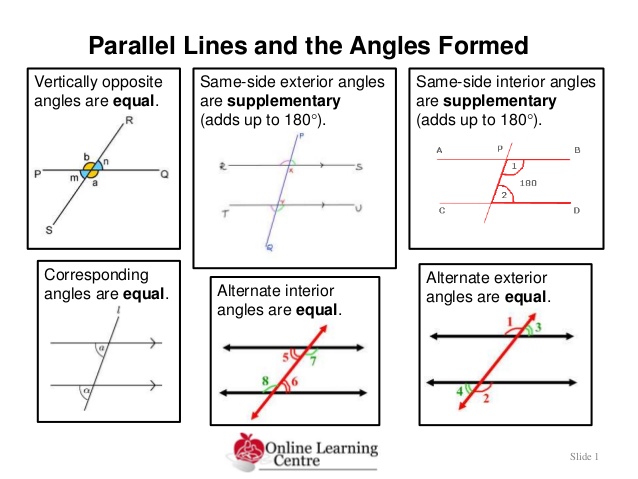
Key ideas:- the cycles of i, -1, -i, 1- conjugate a+bi, a -bi- arithmetic operations of complex numbers- absolute value function and its graph
Homework:-pg 172-173, Ex 1-15-pg 177-179, Ex 1-15-DeltaMath Ch.19 Complex Numbers-DeltaMath Ch. 20 Absolute Value
Next week, we will have a midterm exam. Please download the test at home (will be released next Sunday by noon), and bring your laptop and calculator to class. Please let me know if you will be absent:)
Have a nice evening, and look forward to seeing you all next Sunday!
Best,

Ms. Li

Ms. Lijia Li from Newton South High School Math Department will give a free webinar on 03/17/2024, Sunday, 7:30-8:30 pm.

The following topics will be covered:
-NSHS Math Curriculum
-What do you need to bring to school
-Some learning strategies
-Math Resources
-Math Competitions & Summer Programs
Please fill in this form https://forms.gle/bBpCXMx1BrDqRG2b6 to register for the webinar, and share the questions with Ms. Li ahead.

Look forward to seeing you then!

牛顿南高数学李老师将于 2024 年 3 月 17 日星期日晚上 7:30-8:30 举办面向同学与家长们的公益讲座，将涵盖以下主题：
-南高的数学课程设置
-去学校需要带什么东西
-高效数学学习策略
-课外数学学习资源
-数学竞赛与夏令营
请填写此表以注册参加 https://forms.gle/bBpCXMx1BrDqRG2b6，并提前分享您感兴趣的问题，我们尽量在讲座前把问题整理到slides里。下周日晚同一时间我们还将邀请几位优秀学姐学长交流分享数学/理科学习的心得与经验，敬请期待[Salute][Salute]。

期待届时见！

Dear Students,

Today we reviewed Ch.17 homework and exit ticket and learned Ch.18 Synthetic Division. Please check the online notes for your reference. 
You may also find this page helpful: https://www.cuemath.com/algebra/synthetic-division-of-polynomial/
Homework:

-pg 168-169, Ex 1-14

–DeltaMath Ch.18 Synthetic Division
Next week, there is a free webinar by Prof. Lo. Please see the flyer for more details. 

See you next Sunday!
Best,

Ms. Li

Dear Students,

Today we went over problems in Ch.16 HW and ET 16, and reviewed topics in Ch.17 Quadratics. Please check our notes for your reference.

Key points:

• standard form, vertex form, factored form
• discriminant 
• Vieta’s formula

Homework:

-Textbook pg 158-160, Ex 1-19

–DeltaMath Ch.17 Quadratics

Next week we will learn Ch. 18: Synthetic Division. In case you will not be here next week, here is the digital copy of the Ch.18 exit ticket.

See you next Sunday!

Best,

Ms. Li

Dear Students,
Today we reviewed Ch.15 HW Ex8, 15, 16, and three problems in the ET15. In Ch.16 Functions, students explained Examples 1-6 and Ms. Li explained Examples 7-10 on the board. We also finished Exit Ticket Ch.16 before the end of class today. Please check our online notes for your review. 

Functions:

-domain, range, independent/dependent variables

-asymptotes 

-composition of functions

-vertex (maximum/ minimum)

-zeros, roots, x-intercepts, real solutions

-function translations (translation, reflection, rotation, dilation)

Homework:

-Textbook pg 140-145, Ex 1-32

–DeltaMath Ch.16 Functions 

Look forward to seeing you next week!

Warm regards,

Ms. Li

Dear Students,

First of all, let’s welcome Shuran, our new friend!

Today we discussed some questions in BlueBook Practice 1 and ET 14: Lines. Students also reviewed Examples 1~3 in Ch. 15: Interpreting Linear Models and did Exit Ticket 15 in class. Please check our notes for your review. 

Homework:
1. Textbook pg 128~131, Ex 1~16
2. DeltaMath Ch.15 Interpreting Linear Models
3. ET 15 (if you have not finished it in class)

Last but not least, we found a great website https://www.cracksat.net/digital/math/ and hope you find it helpful. Enjoy!

There will be no classes in the following two weekends (Please check the school calendar here: https://www.newtonchineseschool.org/calendar.php). Wish everyone a lovely Lunar New Year, and I look forward to meeting you again on Feb. 25th!

Warm regards,

Ms. Li

Dear Students, 

Thank you for taking Practice 1 at College Board BlueBook App. Unfortunately, as an Educator Account, I cannot access your data, nor can I see the questions in the practice test. Please share your score with me either in person or by email, so that I can keep track of your progress:)

Please save Practice 2 and 3 for our Mid- and Final- exams in the Spring semester. As you are not allowed to skip English sessions in the practice test, I will ask you to finish the English part at home, and come to school to finish the math part in class for the future Mid- and Final- exams.

Please take screenshots of the questions you want me to explain, and upload them to a shared Google Drive. I can use that to help go over next week.

Homework:-ET 14: Lines
Next week will be the first week of the Spring Term. Please bring your textbook, and we will start Ch. 15. Interpreting Linear Models.

Warm regards,

Ms. Li